- 论文动机调研,主要针对trie树存在的问题
HOT树(主要针对ART树高进行优化)
背景介绍
虽然ART可以实现空间的高利用率,因此可以在整数测试集上实现高性能,但在索引字符串时,它的平均扇度要低得多。这种较低的展开通常发生在树的较低级别,并且是由字符串键中普遍存在的稀疏键分布引起的。(这里我的想法是,索引字符串更像是放松了压缩限制的整数型ART树)
常见的trie树优化思路
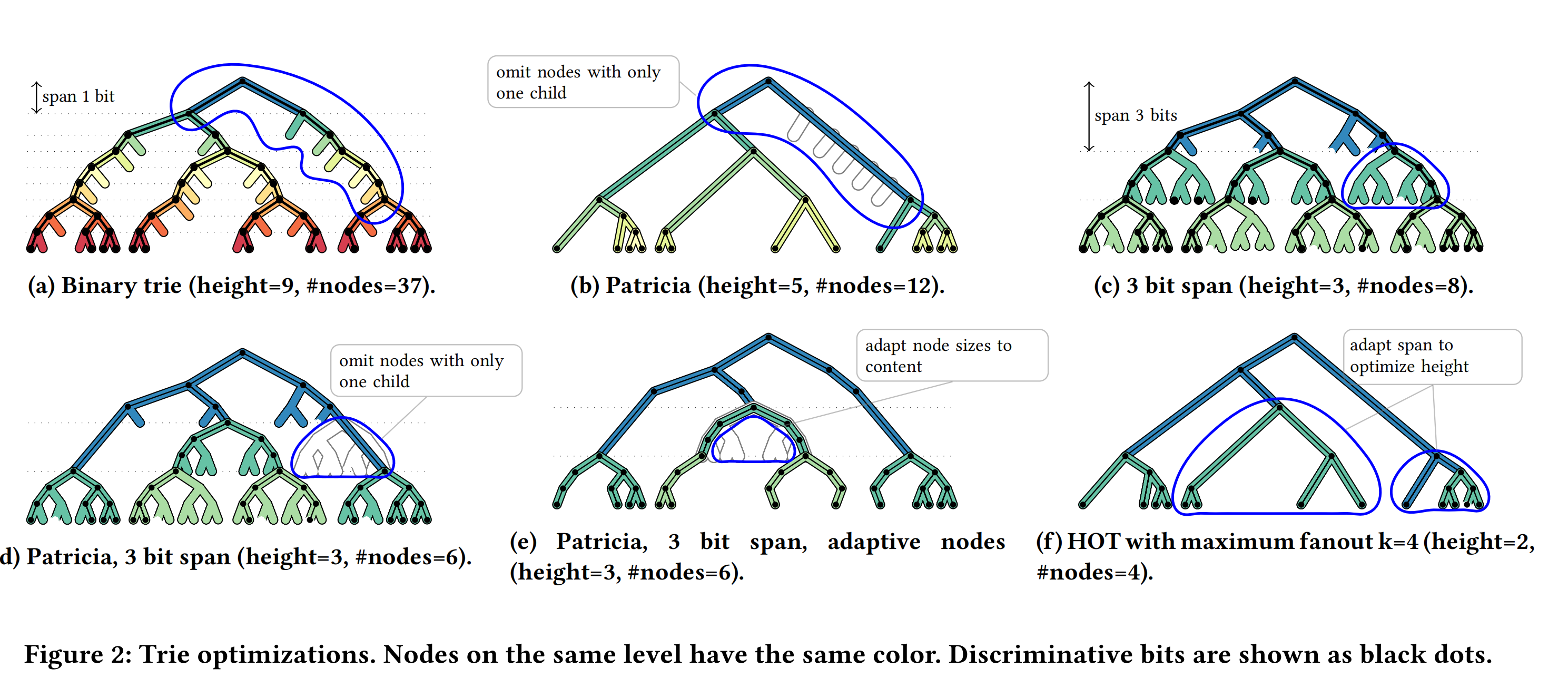
从最简单的binary trie树开始说起,左右孩子节点分别代表了0和1,但是这种设计结构会产生较大的树高并对性能产生影响。人们最初对trie树的优化方案是减小trie树树高。人们最先想到的是把只有一个子节点的父子节点进行合并,这个在图b中有所展示。为了进一步减小树高,人们把每层节点保存的数据位数增加,如图c中所示。这种方案虽然减少了trie树的层高,但是会导致trie树的fanout(也就是空指针数)增加,造成了空间浪费。可以使用图b中的优化方案对c进行优化,但是优化的效果有限,见图d。前几年人们设计出了ART树对方案c进行优化,ART树使用了8bit作为每层节点保存的数据位宽,并且使用了动态大小的节点,节约了空间的同时提高了cache命中率进一步提升了系统性能。然而,虽然ART树有着不错的效果,但是即便在使用了很大的span情况下,ART在底层节点保存的数据会比较稀疏,从而导致出现出现fanout很小的情形。本文作者最后提出了动态调整span来减小树高。
Masstree
背景介绍
作者一共做出了三个贡献:
- 构建了一颗支持并发访问的变种前缀树。
- 设计出了一套每个树节点的数据布局模式,加速了树的层级访问速度。
- 给出了多核心处理树服务具有更好的性能的结论。
- 设计出了一套突出所有的性能瓶颈的评价机制。
乐观锁机制:这是在OLFIT中提出的一种处理并发操作的机制。简单来说就是在读取一段数据之前首先读取其数据版本号,在读取完成后再读取对应的数据版本号,如果版本号相同则完成数据读取操作,如果版本号不同则重试。
设计部分
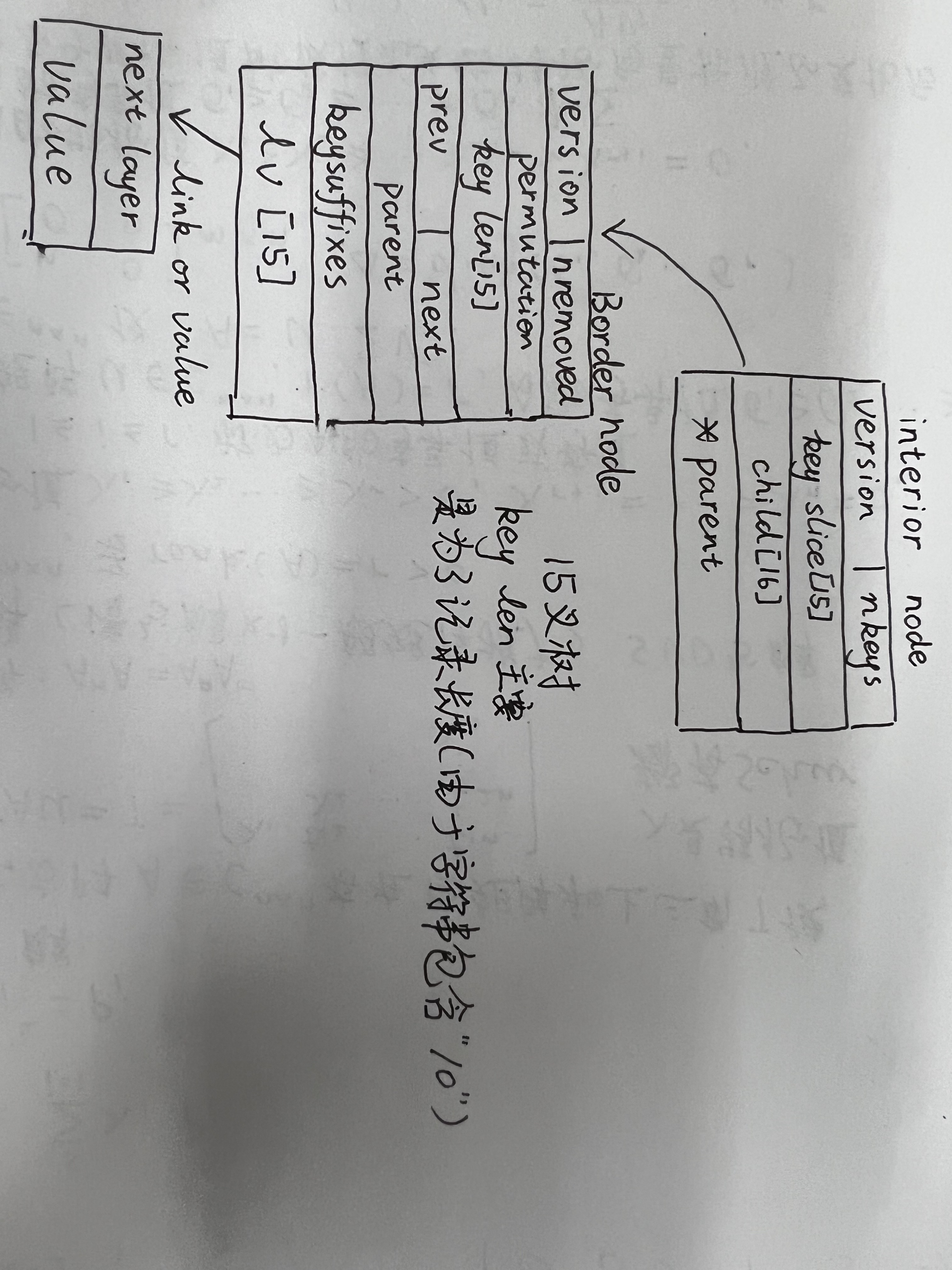
每一层节点存储了8bit的数据宽度。对于每一个节点,内部使用了一个B+树进行存储。节点与节点之间的构造和trie树一致。
给出了一个例子让我们了解数据结构的工作机制:
- 向masstree中插入“01234567AB”,会把该键直接存储在根层(layer0)。具体的存储模式是:会把“01234567”存储,再把“AB”存储。
- 向masstree中插入“01234567XY”,这个键和之前插入的键有大于等于8byte的公共前缀,这个时候masstree必须要新增加一个layer层(layer1),把“AB”和“XY”作为layer1的b+树的叶子节点,01234567指向了layer1中b+树的根节点。
- 删除“01234567XY”,首先在root层搜索01234567,之后进入layer1层找到对应的“XY”进行删除操作,之后“AB”仍旧留在layer1中。
分析masstree的时间复杂度,假设masstree中存储了n个最大长度为l的键,masstree有着和b树一样的时间复杂度。在使用b树保存上述数据的情况下,一次查询时间需要检查O(logn)个节点并且会发生O(logn)次比较,但因为每一个键都有O(l)的长度,总的比较开销是O(l·logn)。一个masstree在每一层中会进行O(logn)次比较,一共有O(l)层,因此总比较次数仍旧是O(l·logn)。如果键有着很长的公共前缀,masstree会是一个比较平衡的树,并且只会发生O(l+logn)次比较开销(这里需要说明的是l是键拥有的公共前缀,logn是键的后缀)。如果在不平衡的负载情况下,masstree会比b+树产生更多的比较开销。
在单线程情况下和b+树的分裂策略是一样的,其中也使用了一些小的优化来提升性能以及节约空间使用率。
总结
阅读了三篇文献:ART(12年),HOT(18年),Masstree(13年)。Trie树在内存数据库中被广泛使用,其中最基本的两个概念:
- span:代表trie树每个节点保存的数据的位宽。
- fanout:代表trie树每个节点拥有的子节点个数的平均值。
提升span能够很好的减少trie树的高度,但是会减少压缩率,span太小会导致树太高,访问层数太多,性能不高。
提升fanout能够减小trie树的高度,但是会浪费空间(比如很多的空指针),fanout太小会导致树太高,访问层数太多,性能不高。
使用学习索引作为fanout的查找模型能够很好的提升读速度,并且结合trie树的数据压缩策略,有效的减小索引所占空间资源。