高维数据索引

想法来源

为什么需要数据库索引

数据存储作为计算机的重要组成部分，经常以条目的形式存储在磁盘等存储设备上。计算机会在需要某些数据的时候从磁盘中把一部分数据加载到内存等高速存储设备中，最简单的方式就是顺序扫描整个磁盘并找到需要的数据，但是这个过程产生的时间开销可能是十分巨大的。

人们为了能够加速数据获取的速度，考虑在内存中建立索引结构。常见的索引结构如B+树（读性能优异，插入更新操作比较耗时），哈希表（查询较快，但是处理哈希冲突以及扩容操作会比较耗时），基数树（空间利用率很高，但是查询以及更新操作比较耗时）等等，每一种数据结构都有自身的优势和劣势，在各自特定的工作场景下有着不错的性能表现。
为什么会考虑高维数据索引

目前使用率最为广泛的索引数据结构B+树，由于能够把数据有序的放在磁盘中，减少了磁盘IO。但是当我们遇到了高维数据时，如何对数据进行排序来减小磁盘IO成了一个大问题。1987年，人们曾提出了基于B树的高维数据索引R树，通过构建最小矩形（MBR）对空间进行分割，保证了在进行数据查询时的空间局部性，减小了磁盘IO。但是，由于R树在构建过程中会发生重叠的MBR，导致额外的查询开销，并且在插入更新的操作过程中产生的时间开销十分巨大，R树的性能表现仍旧有很大的提升空间。
高维数据库的应用场景

常见的GPS，地图查询，高维图片数据存储。在SQLite中使用了R树加速了空间查询操作，常见的地理信息软件也提供了如geopandas等库加速对空间数据的查询访问操作。

传统数据索引总结介绍

索引名称	适用的查询类型	适用的数据类型
B树	点查询	一维数据
B+树	点查询	一维数据
B*树	点查询	一维数据
UB树	点查询，区间查询	一维数据，多维数据
H树	点查询	一维数据
$ST^2B$树	区间查询，knn查询	多维数据
Compact-B树	点查询	一维数据
R树	区间查询	多维数据
R+树	区间查询	多维数据
R*树	点查询，区间查询	空间数据，多维数据
X树	区间查询	多维数据，高维数据
M树	区间查询，knn查询	多维数据
Hilbert-R树	区间查询	多维数据
BR树	点查询，区间查询，覆盖查询，绑定查询	一维数据，多维数据
QR+树	区间查询	大范围的空间数据

学术界调研结果

为了进一步调研学术界对于高维数据的索引构建方法，我首先阅读了近几年针对高维数据索引比较火的一个方向：基于学习索引的高维数据处理介绍，接下来先介绍一篇该领域的文献综述：

A Tutorial on Learned Multi-dimensional Indexes
- 前言
  - 首先介绍了学习索引的来历，以及相比于传统的索引，O(1)复杂度的学习索引更加高效。这里首先讲述了最先提出学习索引的文献：The Handwritten Trie: Indexing Electronic Ink，作者提出使用隐马尔可夫模型建立学习索引。作者把当前学习索引划分了两个研究方向：
  1. 对学习的模型进行索引
  2. 对索引数据进行学习最后得到一个模型
  - 大部分的学习索引结构只能够很好的解决只读场景下的性能要求，但是对于更新操作，目前也有新的方案被提出：ALEX: An Updatable Adaptive Learned Index，这篇文献能够很好的解决更新操作。
  - 传统的高维数据的索引之前已经介绍过，在此不赘述。Sagedb: A learned database system.这个是谷歌提出的基于机器学习的数据库，其中有关于一维和高维数据的索引设计方案但是细节部分没有介绍。
- part1：学习索引
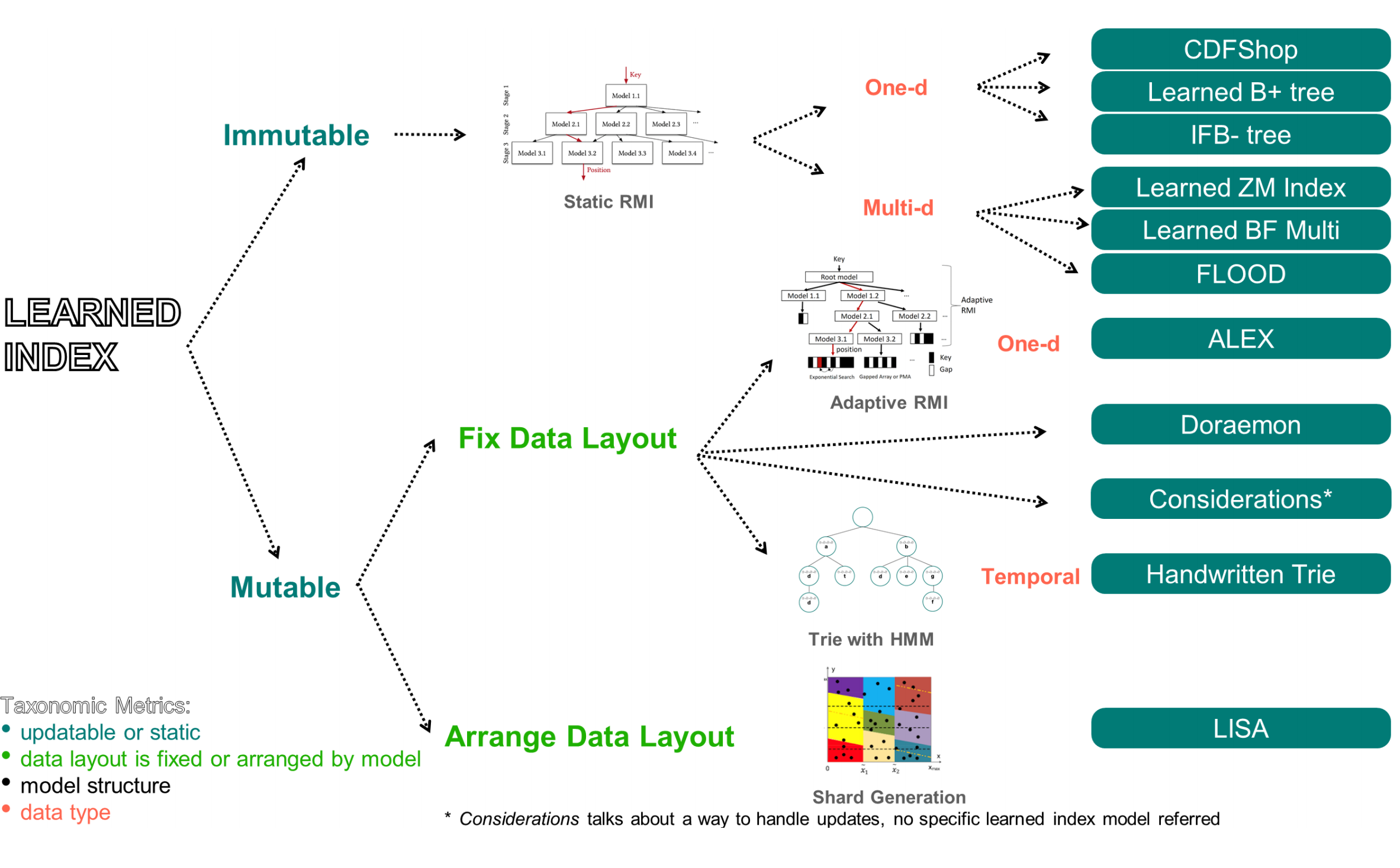
  - 首先介绍了学习索引近几年的开山之作：The Case for Learned Index Structures这篇18年的vldb的文章，首次提出使用学习模型替换一维数据索引B+树的功能。包括从最简单的使用CDF曲线替换索引，以及稍微复杂的使用RMI模型，通过构造一个类似决策树模型的数据结构，提升整个学习索引的预测准确率。单纯学习CDF累计函数曲线这种方案在学习整个数据集之后得到的预测准确率不是很高。为了进一步提升学习索引的准确率，一种回归模型被提出（Recursive Model Index）。该模型的基本思路是，类似于决策树的方式，通过建立多层简单预测模型，不断对预测结果进行修正，保证较高的预测准确率。与此相关的有一篇文献:CDFshop，里面讲述了如何通过设置多层预测模型提升学习索引的正确率，对于寻找到最适合的基本函数以及最高效参数配置，也提出了一套启发式算法进行搜索，最终提供了一套可视化软件，能够直观的反应RMI参数的影响。最终得到的结论是：学习到的索引结构可以提供具有较小内存占用的快速查找时间，但需要进行适当的调优。我们的演示将让观众成员直观地了解RMI的参数如何影响查找延迟和模型大小的权衡。
  - 虽然以上的设计方案在只读情景下的性能远超传统的数据索引。但是数据库中存储的数据集并不是一成不变的，面对需要进行数据更新以及数据删除的情景，之前训练好的CDF函数需要重新进行训练以保证高准确率。针对更新场景，ALEX：An Updatable Adaptive Learned Index这篇文献进行了一个新的设计构想。ALEX专门针对传统的学习索引的不足进行提升，通过对RMI模型进行进一步的修改，实现了对新数据插入功能的支持。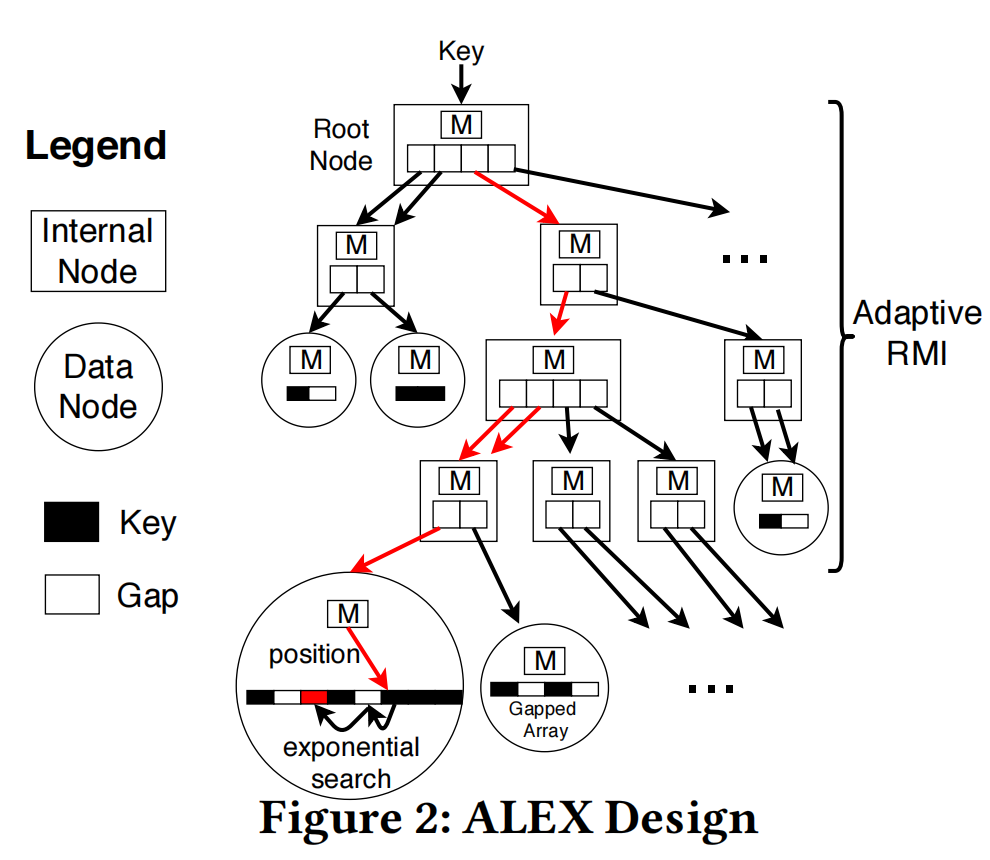上图给出了ALEX的主要设计图，分为中间节点和数据节点，中间节点通过做出CDF曲线，如果某一部分为接近线性分布，就使用一个数据节点表示该区间，添加到原中间节点的子结点中。对于不符合线性分布的区间，就使用一个新的中间节点来表示该区间，并把该新的中间节点添加到原中间节点的子结点中。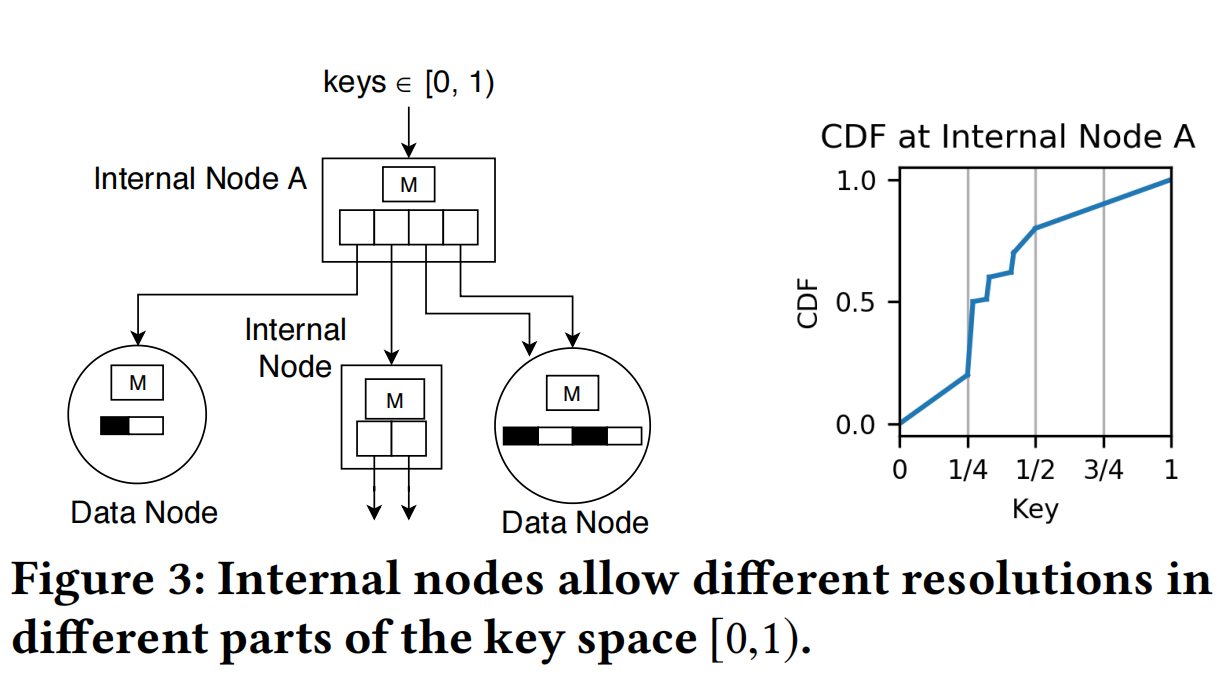上图给出了一个例子，右图给出的是数据分布的CDF曲线，左图是根据上述策略生成的索引结构。此外，ALEX提出了一套节点分裂算法来保证负载的均衡性。通过建立有空隙的数组来满足快速插入的要求。
- part2：高维数据学习索引
  - 基于上面给出的一部分学习索引的例子，作者继续介绍了针对高维数据的学习索引。首先介绍了：The Case for Learned Spatial Indexes，这篇文章主要介绍使用不同的分割算法对二维数据进行分割后（使用了Qg-tree,r-tree分割机制，fix-tree等），分别使用传统的二分查找和机器学习模型(这里提出了radixspline模型，区别于传统的RMI模型)进行查找的性能比较，得出的一个比较有趣的结论是，随着对每个分区包含的目录项数目的增加，查找性能会逐渐提升直到达到一个最佳优化点后才发生下降。针对每一个测试集，作者分别进行了不平衡负载和平衡负载查询测试，在不平衡查找操作过程中性能会下降一个数量级。此外，作者分别测试了基于机器学习模型的不同分割策略的查询延迟和内存使用率。最终得出的结论是，在传统的一维数据中，学习索引取得的效果更好，但是对于高维数据和分割算法有很大的关系，并且相比于传统索引优势没有特别明显。
  - 通过以上的文献，可以快速了解到对于高维数据建立学习索引的难点：
    1. 如何把二维数据存储在一维的磁盘上，目前常见的方法是进行分割（如网格法），在保留一部分数据的局部性的情况下把高维数据映射到一维空间。
    2. 如何解决学习索引对数据的插入，更新，删除等操作后对模型准确率的影响。
    3. 索引预测错误后的修正搜索策略产生的时间开销。
  - 接下来介绍flood，这是专门针对高维数据建立的学习索引策略。
    1. flood采用了常见的分割算法，把二维数据分割成一个个连续的cell，每一个cell中的数据在磁盘上连续的存储。
    2. 查询操作流程：为了查询某个区间内的所有数据，会依次访问重叠cell中的数据，找到每个cell中满足要求的数据区间，对区间内的数据进行线性扫描过滤出所有满足要求的数据，最后把这些cell中的查询结果合并到一起作为结果返回。
    3. 优化网格查询的性能。如何选取网格的大小，以及选择网格排序的方式都能够决定查询的性能好坏。flood使用了一个计算开销的模型来判断查询时间的大小，从而对性能进行评估。
    4. 对于一个给定的数据集，flood提出了四个优化的点：1.对数据集和查询请求进行采样，对RMI模型进行调整。（其实就是保证对于每个维度每个cell中的数据点数量尽量接近，但是最终的cell结果并不是这样，与维度之间的相关性有一定关系）2.迭代的选择网格的排序维度。3.对于每一个可能的维度排序，运行一个梯度下降搜索算法，以找到一个网格大小的最优解，通过上面的开销模型进行计算得到。4.在d个布局中选择目标函数成本最低的布局。
    5. 在计算CDF曲线的时候，使用了PLM，把CDF曲线分割为几段线性函数进行拟合。使用了带有缓存的B树对这些区间以及这些区间中的数据项进行管理。（多维CDF性能并没有好处）